Εμβαδόν
Εμβαδόν είναι η συνολική περιοχή της επιφάνειας ενός τρισδιάστατου αντικειμένου και μετριέται σε τετραγωνικά.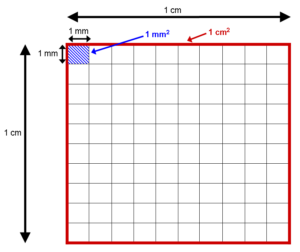
https://en.wikipedia.org/wiki/File:Area_conversion_-_square_mm_in_a_square_cm.png
Μετρητικές μονάδες – Εμβαδόν
1 τετραγωνικό μέτρο = 10 000 τετραγωνικά εκατοστά, cm2
1 εκτάριο = 10 000 τετραγωνικά μέτρα, m2
1 τετραγωνικό χιλιόμετρο= 100 εκτάρια,
1 τετραγωνικό μέτρο = 100 τετραγωνικά δεκατόμετρα, dm2
1 τετραγωνικό δεκατόμετρο = 100 τετραγωνικά εκατοστά, cm2
1 τετραγωνικό εκατοστόμετρο = 100 τετραγωνικά χιλιοστόμετρα, mm2
Τύποι Εμβαδόν
Κύβος |
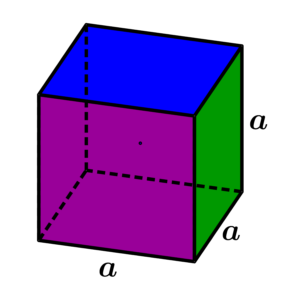 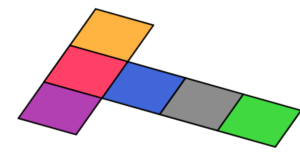 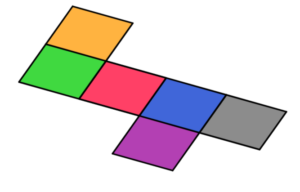 |
Ε Τετραγώνου = a2A = 6 τετραγωνική επιφάνεια A = 6 a2 |
a – μήκος βάσης |
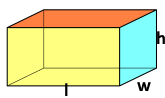
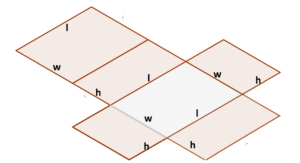
Ορθογώνιο Πρίσμα |
|
|
A = 2lw +2wh + 2lh= = 2(lw +wh+lh) |
l – μήκος, w – πλάτος, h – ύψος |
Τριγωνικό Πρίσμα |
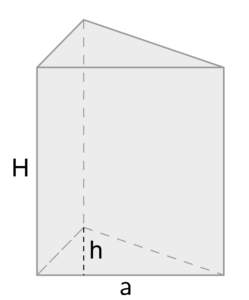 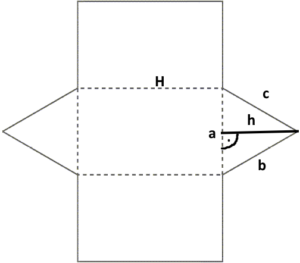 |
SA= LSA + 2 B LSA = aH + bH + cH = =(a + b + c) H = PH
A = 2 (ah/2) + (a+b+c)H =ah+PH |
Ε- ΕμβαδόνB – εμβαδόν τριγωνικής πλευράς, βάσης LSA – Πλευρικό εμβαδόνa – μήκος της μίας πλευράς του τριγώνου,h -το μήκος του υψόμετρου πλευρικά –
|
Ν- γωνο Πρίσμα |
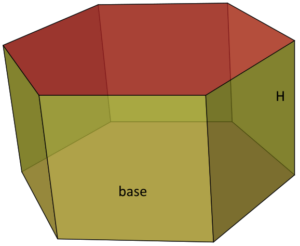 |
SA= LSA + 2 BA =PH + 2B |
SA-E – ΕμβαδόνB – Βάση LSA – Πλευρικό ΕμβαδόνB – εμβαδόν βάσης (εμβαδόν κανονικόυ πολύγωνου)
|
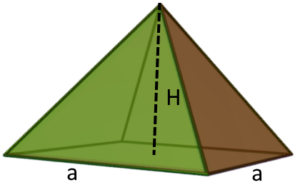
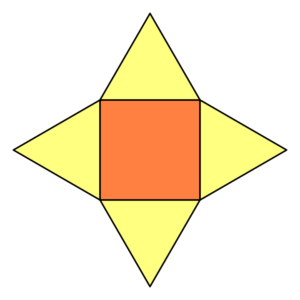
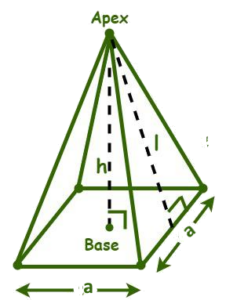
Τετραγωνική Πυραμίδα |
|
|
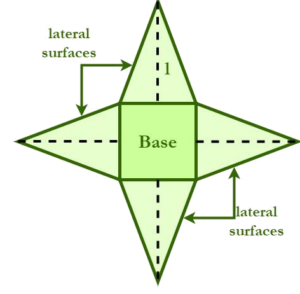
SA= LSA + B A = B + 1/2 x P x l P = 4a LSA =1/2 x P x l= = 1/2 x 4a x l =2al B = a2 Lateral surface area of a pyramid (LSA) = Sum of areas of the lateral surfaces of the pyramid |
SA – Ε- ΕμβαδόνLSA – Πλευρικό εμβαδόν a -μήκος πλευρών βάσηςH – κάθετο ύψος, ύψος της πυραμίδαςB – εμβαδόν βάσης πυραμίδαςP – περίμετρος βάσης l – μήκος κλίσης των πλευρών (μήκος απ’ τη βάση ως την κορυφή) |
Τριγωνική Πυραμίδα |
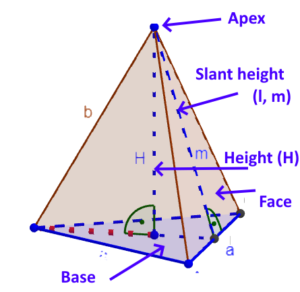 |
SA= LSA + B SA = B + 1/2 x P x l LSA =1/2 x P x l Bases area = polygon area Lateral surface area of a pyramid (LSA) = Sum of areas of the lateral surfaces (triangles) of the pyramid |
SA – Ε- Εμβαδόν (surface area)LSA – Πλευρική επιφάνεια B – εμβαδόν βάσης P – Περίμετρος Βάσης H -Κάθετο ύψος, το ύψος της πυραμίδαςa -μήκος πλευράς βάσηςl (m) – μήκος κλίσης των πλευρών. εμβαδόν Βάσης = εμβαδόν πολυγώνου |
Σφαίρα |
 |
Ε = 4πr2 |
r – ακτίνα
|
Απόλυτα κυκλικός κώνος |
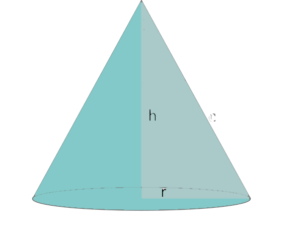 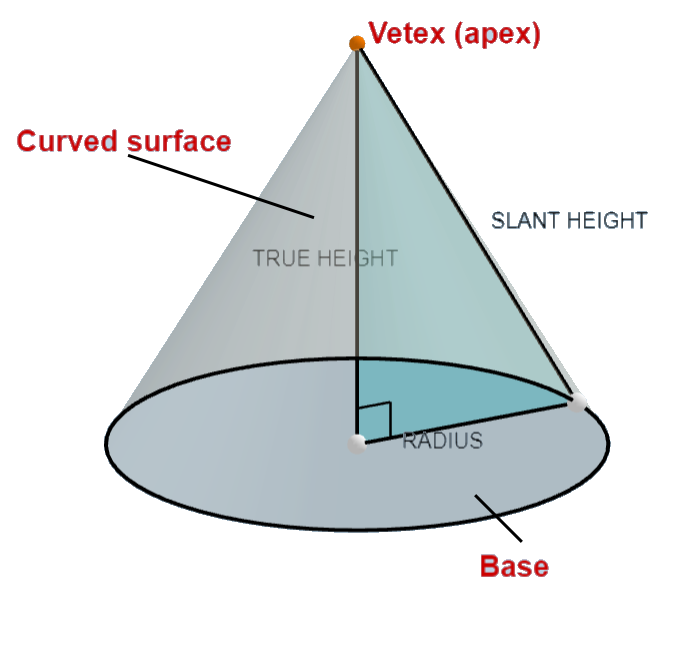 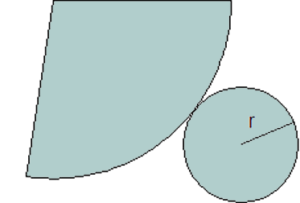 |
Ολικό Εμβαδόν Κώνου= Εμβαδόν κωνικής περιοχής + Εμβαδόν βάσης |
B – Εμβαδόν ΒάσηςH, h – κάθετο ύψος, το Ύψος του κώνουr – ακτίνα
|
Κύλινδρος |
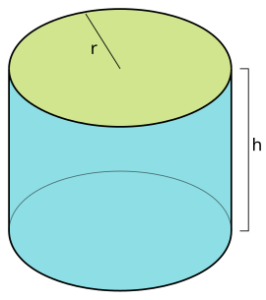 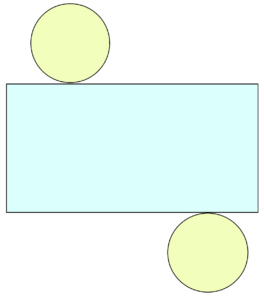 |
Area = 2 · the area of the base + base circumference · height A = 2πr2 + 2πrh |
B – εμβαδόν βάσης
|