Võrdhaarne kolmnurk

Võrdhaarne kolmnurk on kolmnurk, mille on kaks külge on võrdse pikkusega. 

Võrdsete pikkustega külgi nimetatakse  võrdhaarse kolmnurga haaradeks ja
kolmandat külge nimetatakse aluseks. 

Võrdhaarse kolmnurga alusnurgad on võrdsed ja tipunurga poolitaja poolitab aluse ja on alusega risti.

∠ACB = γ on tipunurk.
∠BAC = α ja ∠ABC = β  on alusnurgad,
Võrdhaarse kolmnurga alusnurgad on võrdsed: ∠BAC = ∠ABC.


Võrdhaarse kolmnurga haarad on võrdsed.
AC = BC

Lõik CD poolitab tipunurga ∠ACB.
∠ACD = ∠BCD


CD on tipunurga poolitaja, mis on alusega AB risti ja poolitab aluse.
CD ⊥ AB
AD = DB

Võrdhaarse kolmnurga alusnurga leidmine:
∠A = ∠B = (180º – ∠C) : 2

Võrdhaarse kolmnurga tipunurga leidmine:
∠C = 180º -∠A – ∠B  =180 º – (∠A + ∠B)

 

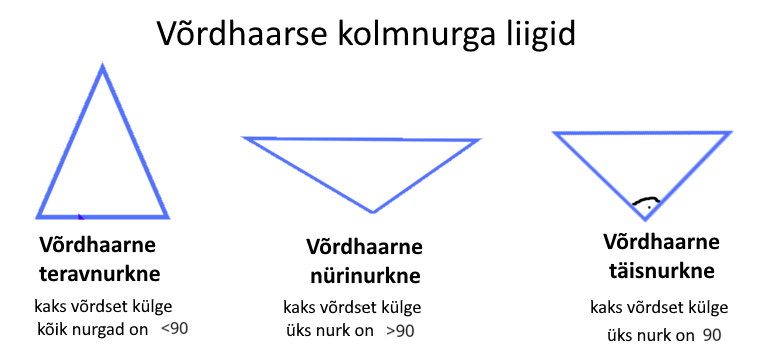
Võrdhaarse kolmnurga liigid:
 – võrdhaarne tervanurkne kolmnurk (kõik nurgad on teravnurgad).
– võrdhaarne nurinurkne kolmnurk (üks nurk on nürinurk).
– võrdhaarne täisnurkne kolmnurk (üks nurk on täisnurk ehk 90° ja teised nurgad on 45°).
Võrdhaarse kolmnurga eriliik on võrdkülgne kolmnurk, mille kõik kolm külge on võrdsed ja kõik nurgad on 60°.

---

 

 

---