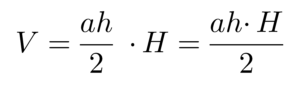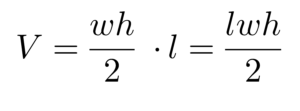Prisma

Prisma 

Prisma on ruumiline kujund, millel on kaks põhitahku, mis on omavahel võrdsed ja asuvad paralleelsetel tasanditel. Põhitahke ühendavad külgtahud. Prisma on hulktahukas. 
Prismat, mille kõigi külgede tasandid ristuvad põhjade tasandiga, nimetatakse püstprismaks. Vastupidisel juhul nimetatakse prismat kaldprismaks. 
Prismasid võib eristada ka nende põhjade kuju järgi: kolmnurkne prisma, nelinurkne prisma jne. 
Risttahukas on nelinurkne püstprisma, mille põhjaks on ristkülik.

Videost saad rohkem teada geomeetria kohta: 

Ruumala valemid

Kuup
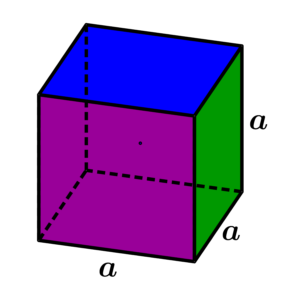a –  külje pikkus
Risttahukas

V = l ⋅ w ⋅ h
või 
V = abc
a=l – pikkus,
b =w –  laius,
h – kõrgus
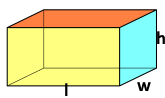
Kolmnurkne prisma

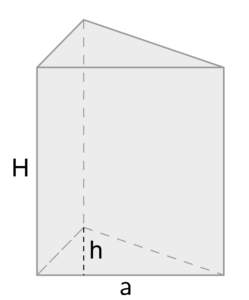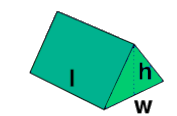V = kolmnurga pindala x prisma kõrgus
a – kolmnurga alus,
h – põhje kõrgus, kolmnurga kõrgus
H – põhjade vaheline kaugus, prisma kõrgus

w = a, l = H

l – põhjade vaheline kaugus
w – kolmnurga alus
h – kolmnurga kõrgus
n-nurkne prisma
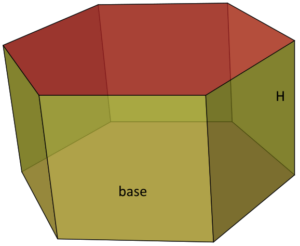 V = B H
või
V = SpH
B =Sp – põhja pindala
H –  prisma kõrgus



Täispindala valemid

Kuup
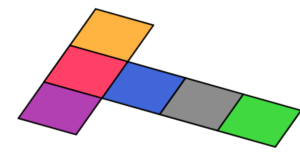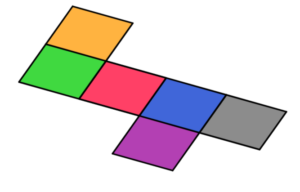St = a2
Täispindala = 6 x ruudu pindala
 St = 6 a2
a – kuubi serv
Risttahukas

Sp = 2lw +2wh + 2lh=
= 2(lw +wh+lh)
St = 2ab +2bh + 2ah=
= 2(ab +bh+ah)
l = a- pikkus,
w = b –  laius,
h – kõrgus
St – täispindala
Kolmnurkne prisma

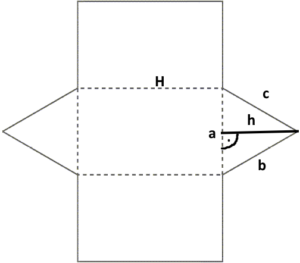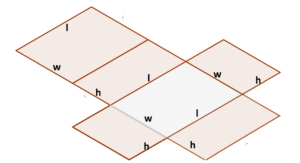
St= Sk + 2

Sp

Sk = aH + bH + cH =
=(a + b + c) H  = PH
Põhja pindala (kolmnurga pindala) 

 

St = 2 (ah/2) + (a+b+c)H =ah+PH

St – täispindala

Sp

– põhja pindala (kolmnurga pindala)
Sk – külgpindala

a – kolmnurga alus,

h – kolmnurga kõrgus
H – prisma kõrgus, põhjade vaheline kaugus

P –  kolmnurga ümbermõõt, põhja ümbermõõt

a, b, c – kolmnurga küljed, põhja küljed
n-nurkne prisma
St= Sk + 2

Sp=PH +2Sp

St – täispindala

Sp – põhja pindala (hulknurga pindala)

Sk – külgpindala
H –  prisma kõrgus

P- põhja ümbermõõt (hulknurga ümbermõõt)